Birth Death Process

Consider the checkout counter example. The states are represented by the number of people currently being processed, and we always move $n$ to $[n-1, n, n+1]$, i.e., either the people in the queue decrease by one, remain same or increase by one. Let the probability for moving up be $p$ and moving down be $q$.

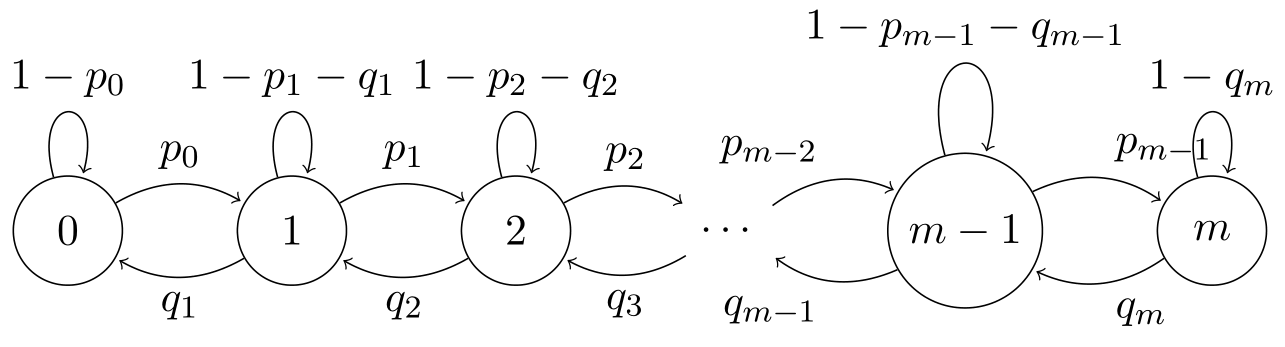
Let’s estimate the steady state probabilities. Consider the following diagram splitting the chain into two parts through the two adjacent states

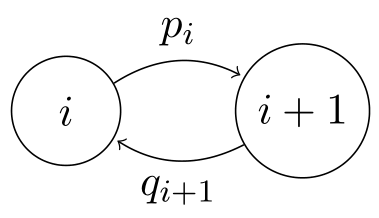
In this case, to maintain steady state, long term frequency of left-right transition should be same as right left transition, i.e., $\pi_{i}p_{i} = \pi_{i+1}q_{i}$ because between any two transitions of type $i \to i + 1$, exactly one transition $i + 1 \to i$ must have occurred due to the structure of the chain.

In the special case of $p_{i} = p$ and $q_{i} = q \;\forall\; i$, \begin{align} \rho &= \frac{p}{q} \quad\text{load factor}\newline \pi_{i+1} &= \pi_{i} \frac{p}{q} = \pi_{i} \rho \newline \pi_{i} &= \pi_{0} \rho^{i} \quad\text{$i = 0,\ldots,m$} \newline \text{Using } \sum_{i=0}^{m} \pi_{0}\rho^{i} &= 1,\newline \pi_{0} &= \frac{1}{\sum_{i=0}^{m} \rho^{i}}\newline \text{if $p < q$ and $m \rightarrow \infty,$}\newline \pi_{0} &= 1 - \rho \newline \pi_{i} &= (1-\rho)\rho^{i}\newline E[X_{n}] &= \frac{\rho}{1-\rho} \quad\text{Exponential Distribution} \end{align} When $\rho = 1$ or $p = q$, then all states are equally likely - symmetric random walk.